Rozpoznawanie 26 liter
Rozpoznawanie liter jest rozszerzeniem poprzedniego przykładu z czterema znakami i stanowi już poważne zadanie do zrealizowania z wykorzystaniem sztucznej sieci neuronowej. Litery są utworzone na matrycy 5 x 7 czyli na 35 polach. I tyle wejść ma sieć. Ponieważ liter jest 26 wobec tego prawidłowe rozpoznanie litery będzie polegało na uaktywnieniu jednego z 26 wyjść sieci, lub więcej w przypadku rozponania w prezentowanym wektorze cech kilku liter.
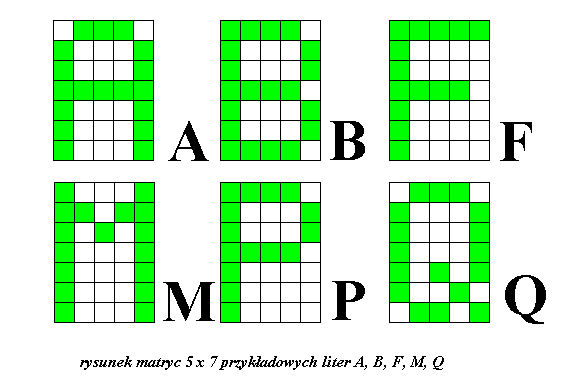
Poniższa tabela przedstawia matryce 26 liter po konwersji zero-jedynkowej:
0 1 1 1 0
1 0 0 0 1
1 0 0 0 1
1 1 1 1 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
|
1 1 1 1 0
1 0 0 0 1
1 0 0 0 1
1 1 1 1 0
1 0 0 0 1
1 0 0 0 1
1 1 1 1 0 |
0 1 1 1 0
1 0 0 0 1
1 0 0 0 0
1 0 0 0 0
1 0 0 0 0
1 0 0 0 1
0 1 1 1 0 |
1 1 1 1 0
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 1 1 1 0 |
1 1 1 1 1
1 0 0 0 0
1 0 0 0 0
1 1 1 1 0
1 0 0 0 0
1 0 0 0 0
1 1 1 1 1 |
1 1 1 1 1
1 0 0 0 0
1 0 0 0 0
1 1 1 1 0
1 0 0 0 0
1 0 0 0 0
1 0 0 0 0 |
0 1 1 1 0
1 0 0 0 1
1 0 0 0 0
1 0 1 1 1
1 0 0 0 1
1 0 0 0 1
0 1 1 1 0 |
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 1 1 1 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1 |
0 1 1 1 0
0 0 1 0 0
0 0 1 0 0
0 0 1 0 0
0 0 1 0 0
0 0 1 0 0
0 1 1 1 0 |
1 1 1 1 1
0 0 0 0 1
0 0 0 0 1
0 0 0 0 1
0 0 0 0 1
1 0 0 0 1
0 1 1 1 0 |
1 0 0 0 1
1 0 0 1 0
1 0 1 0 0
1 1 0 0 0
1 0 1 0 0
1 0 0 1 0
1 0 0 0 1 |
1 0 0 0 0
1 0 0 0 0
1 0 0 0 0
1 0 0 0 0
1 0 0 0 0
1 0 0 0 0
1 1 1 1 1 |
1 0 0 0 1
1 1 0 1 1
1 0 1 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1 |
1 0 0 0 1
1 0 0 0 1
1 1 0 0 1
1 0 1 0 1
1 0 0 1 1
1 0 0 0 1
1 0 0 0 1 |
0 1 1 1 0
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
0 1 1 1 0 |
1 1 1 1 0
1 0 0 0 1
1 0 0 0 1
1 1 1 1 0
1 0 0 0 0
1 0 0 0 0
1 0 0 0 0 |
0 1 1 1 0
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 1 0 1
1 0 0 1 0
0 1 1 0 1 |
1 1 1 1 0
1 0 0 0 1
1 0 0 0 1
1 1 1 1 0
1 0 1 0 0
1 0 0 1 0
1 0 0 0 1 |
0 1 1 1 0
1 0 0 0 1
1 0 0 0 0
0 1 1 1 0
0 0 0 0 1
1 0 0 0 1
0 1 1 1 0 |
1 1 1 1 1
0 0 1 0 0
0 0 1 0 0
0 0 1 0 0
0 0 1 0 0
0 0 1 0 0
0 0 1 0 0 |
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
0 1 1 1 0 |
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
0 1 0 1 0
0 0 1 0 0 |
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 1 0 1
1 0 1 0 1
0 1 0 1 0 |
1 0 0 0 1
1 0 0 0 1
0 1 0 1 0
0 0 1 0 0
0 1 0 1 0
1 0 0 0 1
1 0 0 0 1 |
1 0 0 0 1
1 0 0 0 1
0 1 0 1 0
0 0 1 0 0
0 0 1 0 0
0 0 1 0 0
0 0 1 0 0 |
1 1 1 1 1
0 0 0 0 1
0 0 0 1 0
0 0 1 0 0
0 1 0 0 0
1 0 0 0 0
1 1 1 1 1 |
|
|
Liniowym rozwinięciem tych matryc będš wektory wejściowe ciągu uczącego.
Ciąg uczący składa się z 26 następujących wektorów uczących :
Wektor wejściowy - 35 wartości
Wektor wyjściowy - 26 wartości
0 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 1 1 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 1 1 0
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 1 1 0
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 1 1 1 0
0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 0 0 0 0 1 0 0 0 0 1 1 1 1 0 1 0 0 0 0 1 0 0 0 0 1 1 1 1 1
0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 0 0 0 0 1 0 0 0 0 1 1 1 1 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 0 1 0 0 0 1 1 0 0 0 0 1 0 1 1 1 1 0 0 0 1 1 0 0 0 1 0 1 1 1 0
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 1 1 1 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1
0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 1 1 0
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 1 1 0
0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 1 1 0 0 1 0 1 0 1 0 0 1 1 0 0 0 1 0 1 0 0 1 0 0 1 0 1 0 0 0 1
0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 1 1 1 0 1 1 1 0 1 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 0 0 0 1 1 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 0 1 1 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 1 1 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
0 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 1 1 0 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 1 1 0 1 0 1 0 0 1 0 0 1 0 1 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
0 1 1 1 0 1 0 0 0 1 1 0 0 0 0 0 1 1 1 0 0 0 0 0 1 1 0 0 0 1 0 1 1 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
1 1 1 1 1 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0
1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 0 1 1 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 0 1 0 1 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
1 0 0 0 1 1 0 0 0 1 0 1 0 1 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 1 1 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0
1 0 0 0 1 1 0 0 0 1 0 1 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
1 1 1 1 1 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
Prawidłowe ustalenie ilości warstw ukrytych i neuronów w tych warstwach jest już trudniejsze niż w przykładach poprzednich. W wyniku przeprowadzonych prób okazało się, że konieczna jest jedna warstwa ukryta. Sieć rozwiązuje to zadanie prawidłowo, jeżeli ilość neuronów w tej warstwie jest większa od 8 (nie przekraczano 30). Natomiast sieć uczy się najszybciej jeżeli tych neuronów jest 10. Schemat sieci wygląda zatem następujšco:
35 - 10 - 25
Tak nauczona sieć prawidłowo rozpoznaje wzorce prezentowane do nauki, ale także doskonale sobie radzi z rozpoznawaniem liter zniekształconych.
Sprawdzianem nauczenia sieci będzie rozwiązanie następującego problemu:
Zostaną wygenerowane wektory wejściowe, obrazujące ewolucję matrycy litery B do matrycy litery H tak, aby w pewnym momencie nastąpiło przybliżenie matrycy litery A. Wektorów takich będzie 12. Wyniki należy zinterpretować w ten sposób, że im większa będzie wartość liczbowa na wyjściu sieci odpowiadającemu danej literze, tym więcej cech danej litery w zaprezentowanej matrycy (wektorze wejściowym) sieć rozpoznała.
Otrzymane wyniki
W tabeli poniżej zaprezentowano otrzymane wyniki. W pierwszej kolumnie pokazane są litery, a w odpowiadających im
rzędach wartości, jakie uzyskano na wyjściach sieci prezentując jej wektor wejściowy wygenerowany na podstawie matrycy znaku pokazanego nad daną
kolumną. Odcieniami szaroci wyróżniono poziom rozpoznania cech litery.
Widać, iż nauczona sieć bardzo poprawnie rozpoznaje przezentowane wzory, nawet zniekształcone, ale także dostrzega w nich i inne litery. Na tej
podstawie można dokładnie badać jakie cechy liter zostały uznane przez siec za istotne dla opisu litery.
Zwiększenie precyzji rozpoznawania liter czy też szerzej - znaków i symboli opartych na matrycy prezentowanej sieci można uzyskać poprzez np.
powiększenie jej rozmiarów i jednocześnie odpowiednio definiując okno dyskryminatora filtrującego wyniki.
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
0.020985 |
0.304754 |
0.553698 |
0.982967 |
0.993287 |
0.984049 |
0.969733 |
0.663561 |
0.059392 |
0.036503 |
0.030628 |
0.011370 |
B |
0.943860 |
0.901880 |
0.249863 |
0.355721 |
0.979239 |
0.471022 |
0.061320 |
0.000184 |
0.000960 |
0.000015 |
0.000081 |
0.000020 |
C |
0.000106 |
0.000014 |
0.000011 |
0.000001 |
0.000021 |
0.000030 |
0.000014 |
0.000024 |
0.000097 |
0.000011 |
0.000001 |
0.000004 |
D |
0.000378 |
0.000031 |
0.000181 |
0.000031 |
0.000003 |
0.000032 |
0.000006 |
0.000035 |
0.000013 |
0.000159 |
0.000038 |
0.000078 |
E |
0.003512 |
0.005860 |
0.001913 |
0.000090 |
0.000241 |
0.000172 |
0.000150 |
0.000169 |
0.000808 |
0.000312 |
0.000770 |
0.001932 |
F |
0.000009 |
0.000164 |
0.000346 |
0.000430 |
0.000040 |
0.000060 |
0.000133 |
0.000329 |
0.000090 |
0.000891 |
0.004434 |
0.002915 |
G |
0.000008 |
0.000001 |
0.000038 |
0.000007 |
0.000010 |
0.000055 |
0.000168 |
0.000122 |
0.000107 |
0.000020 |
0.000002 |
0.000001 |
H |
0.000183 |
0.002419 |
0.002891 |
0.046080 |
0.001623 |
0.003613 |
0.010833 |
0.368816 |
0.078445 |
0.705525 |
0.850262 |
0.934215 |
I |
0.000230 |
0.000092 |
0.000062 |
0.000041 |
0.000195 |
0.000122 |
0.000100 |
0.000047 |
0.000102 |
0.000021 |
0.000008 |
0.000008 |
J |
0.000781 |
0.000500 |
0.000644 |
0.001639 |
0.001984 |
0.001319 |
0.000535 |
0.000128 |
0.000050 |
0.000030 |
0.000037 |
0.000018 |
K |
0.000002 |
0.000006 |
0.000004 |
0.000002 |
0.000001 |
0.000002 |
0.000002 |
0.000015 |
0.000035 |
0.000078 |
0.000066 |
0.000286 |
L |
0.000005 |
0.000002 |
0.000002 |
0.000000 |
0.000000 |
0.000001 |
0.000001 |
0.000013 |
0.000042 |
0.000076 |
0.000025 |
0.000112 |
|
M |
0.000125 |
0.000024 |
0.000038 |
0.000002 |
0.000002 |
0.000013 |
0.000036 |
0.000683 |
0.011826 |
0.012279 |
0.000983 |
0.009809 |
|
N |
0.001036 |
0.008396 |
0.009188 |
0.000350 |
0.001358 |
0.000859 |
0.007448 |
0.003398 |
0.035541 |
0.006024 |
0.012997 |
0.019950 |
|
O |
0.025499 |
0.001210 |
0.000757 |
0.028576 |
0.563501 |
0.256047 |
0.021712 |
0.000138 |
0.000025 |
0.000000 |
0.000000 |
0.000000 |
|
P |
0.008225 |
0.242688 |
0.020055 |
0.160864 |
0.389486 |
0.060194 |
0.098678 |
0.012626 |
0.011509 |
0.004213 |
0.033683 |
0.002880 |
|
Q |
0.000001 |
0.000000 |
0.000000 |
0.000000 |
0.000000 |
0.000001 |
0.000000 |
0.000000 |
0.000000 |
0.000000 |
0.000000 |
0.000000 |
|
R |
0.001217 |
0.001683 |
0.000614 |
0.084226 |
0.046226 |
0.025855 |
0.001702 |
0.001221 |
0.000092 |
0.000244 |
0.000280 |
0.000216 |
|
S |
0.025307 |
0.018640 |
0.002624 |
0.001936 |
0.075274 |
0.008342 |
0.002550 |
0.000161 |
0.001068 |
0.000008 |
0.000018 |
0.000010 |
|
T |
0.000016 |
0.000075 |
0.000044 |
0.000394 |
0.000260 |
0.000106 |
0.000085 |
0.000022 |
0.000009 |
0.000011 |
0.000032 |
0.000011 |
|
U |
0.000114 |
0.000007 |
0.000005 |
0.000001 |
0.000001 |
0.000003 |
0.000009 |
0.000077 |
0.003268 |
0.000815 |
0.000182 |
0.000288 |
|
V |
0.000502 |
0.000876 |
0.000715 |
0.003565 |
0.001221 |
0.000848 |
0.001024 |
0.001028 |
0.000812 |
0.001420 |
0.002378 |
0.002122 |
|
W |
0.000024 |
0.000011 |
0.000489 |
0.000090 |
0.000020 |
0.000230 |
0.000632 |
0.004148 |
0.000718 |
0.005261 |
0.000488 |
0.000228 |
|
X |
0.000056 |
0.000702 |
0.000305 |
0.000020 |
0.000099 |
0.000036 |
0.000097 |
0.000038 |
0.000157 |
0.000043 |
0.000203 |
0.000343 |
|
Y |
0.000050 |
0.000186 |
0.000099 |
0.000053 |
0.000045 |
0.000041 |
0.000104 |
0.000181 |
0.000355 |
0.000366 |
0.000732 |
0.000558 |
|
Z |
0.000010 |
0.000012 |
0.000010 |
0.000006 |
0.000005 |
0.000005 |
0.000005 |
0.000006 |
0.000007 |
0.000007 |
0.000010 |
0.000013 |
Na tej podstawie można sformułować kolejne problemy w rozpoznawaniu znaków:
powiększyć matryce znaków do np. 8 x 8, 9 x 14, 16 x 16 itp.
rozszerzyć ciąg uczący o cyfry i narodowe znaki diakrytyczne
pisma odręcznego np. w polu o ściśle określonych rozmiarach (przykładem jest kod pocztowy wpisywany w kratki na kopertach listowych)
